Introduction to Finite Automata

All languages in the theory of computation check if a particular string belongs to the language. This is also known as Set membership.

A finite automata is a model of a simple computing device that acts as a language acceptor and is mostly used to detect patterns.

The output this machine produces to any input is either Yes or No and therefore the languages that this machine accepts are known as recursive languages.

Each character from the input string is fed into the machine and at the end of the string if it is the correct input, the string is accepted otherwise it is not.

For example,

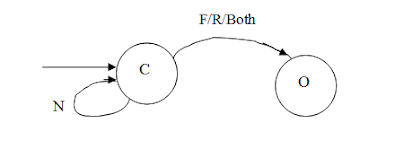
Let us take the example of a door controller,

Suppose we have to design a door controller. The door can either be open or close.

So open and close are the two states in this problem.

What is a State?

A state is a level of achievement.

Now the door has to open,

 1) If there is no one at the front or rear end when the door is closed, the door should remain closed. When there is no one lets denote it as N.

2) But if there is someone at the front (denoted as F) or someone at rear (denoted by R) then the door has to open. 

Now if the door is open and

1) If someone is at the front or rear, the door has to remain open.

2) If there is no one at the front or rear, the door has to close

Therefore the final FA for this door controller problem is

Another example

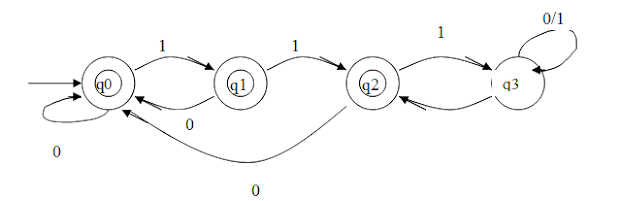
Construct a FA that rejects strings that has more than 2 consecutive 1’s (Alphabet {0,1})

1) If we get a 0, we stay in the same start state q0.

2) After getting 1 for the first time, we move to state q1.

3) On state q1 if we get a 0, we go back to start state q0.

4) On state q1 if we get a 1, we move to state q2.

5) On state q2 if we get a 0, we go back to start state q0.

6) On state q2 if we get a 1, we move to state q3.

7) On state q3 if we get a 1 or 0 we stay at the same state as, we have come across 2 consecutive 1’s and the string has to be rejected.

Therefore we consider the start state q0, state q1 and state q2 as the final states (denoted by a double circle)

This can also be represented in a table as follows

	0	1
q0	q0	q1
q1	q0	q2
q2	q0	q3
q3	q3	q3

Draw a FA that accepts strings that have substring 101 or 110. (Alphabet {0,1})

1) If on the start state q0 we get a 0, we remain at q0

2) If we get a 1, we move to next state q1.

3) At q1 if we get a 0, move to q2. And if we get a 1, move to q3 (we are detecting the sequence 101 through state q2 and sequence 110 through state q3)

4) If at q2 if we get a 0, go back to start state q0 or if we get a 1 at q2 move to q4 (final state) - sequence 101 is detected.

5) If at q3 if we get a 1 stay at q3 or if we get a 0 move to q4 (final state) – sequence 110 is detected.

	0	1
q0	q0	q1
q1	q2	q3
q2	q0	q4
q3	q4	q3
q4	q4	q4

Feel free to comment if you still have any doubts.