Deterministic and Non deterministic FA

A finite automata can be classified as Deterministic finite automata and Non deterministic finite automata.

A deterministic finite automata is practically implementable and can be used in real life problems. In this type of FA, on one state and on one input we can go only to one state.

DFA is defined as a 5 tuple {Q , Ʃ , δ , q₀ , F} where,

Q is the states

Ʃ is the input alphabet

δ is the transition table

q₀ is the start state

F is the set of all final states.

For example if we want to make a DFA for the set of strings 0,1,2 where we have any number of 0’s , followed by any number of 1’s followed by any number of 2’s. The string 00112 has to be accepted by the machine and strings 1102 has to be rejected by the machine.

The DFA for this problem would be as follows.

A non deterministic finite automata is not practically implementable but it is easier to model. In this type of FA, on one state and on one input we can go to multiples states and we can also go to any other state on a nothing (ε). You can stay in multiple states at the same time.

An NFA can be converted into a DFA using an algorithm.

An NFA is defined as a 5 tuple {Q , Ʃ U ε₀ , δ , q₀ , F } where,

Q is the states

Ʃ is the input alphabet

ε₀ is epsilon ( also referred to as nothing)

δ is the transition table

q₀ is the start state

F is the set of all final states.

An NFA for the same example above would be as follows

Here we can be in 2 states at the same time, so on a zero we can be in q0 and q1. But if the string ends at 0, on a nothing ε we can also be in q1 and also in q2 which is the final state.

Another example

Draw a DFA and NFA that accepts strings that end in 1

DFA

1) If on state q0 we get a 0, we stay at q0, which is not a final state as the string has to end at a 1.

2) If on state q0, we get a 1, we go to q1.

3) On state q1, if we get a 0, we go back to q0.

4) If we get a 1 on q1, we stay at q1.

	0	1
q0	q0	q1
q1	q0	q1

NFA

1) Here on state q0, we can go on 2 states, either remain at q0 or go to q1 on a 1 

	0	1
q0	q0	q0, q1
q1	-	-

Another example

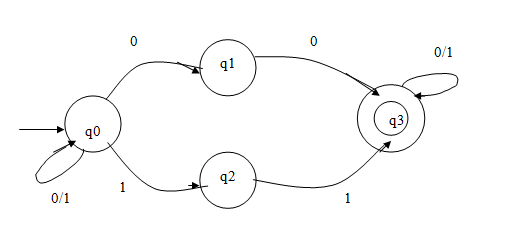
Draw a DFA and NFA which contains strings in 0 and 1 that must contain a double letter.

DFA

1) On state q0, if we get a 0, move to q1 and if we get a 1 move to q2.

2) If on q1 we get a 0, move to q1 and if on q2 we get a 1, move to q1. (This continues until we get a double letter)

3) Once we get a double letter (either 00 or 11) move to q3 and that is the final state.

	0	1
q0	q1	q2
q1	q3	q2
q2	q1	q3
q3	q3	q3

NFA

1) Here we stay on q0 and q1 until we get a double 0, and once we get a double 0 we go to q3, and that is the final state.

2) We stay on q0 and q2 until we get a double 1, and once we get a double 1 we go to q3, and that is the final state.

	0	1
q0	q0,q1	q0,q2
q1	q3	-
q2	-	q3
q3	q3	q3

Feel free to comment below, if you still have some doubts. 

Recommended Articles:

Introduction to Finite Automata

Examples on constructing NFA and DFA