Every RE of an FA can be written as a Regular grammar and every regular grammar can be converted to a FA. Regular grammar is subset of CFG. So problems that can be solved by an FA can also be solved by a Pushdown Automata (for which the grammar required is CFG).
Regular grammar has only 2 symbols on the right, one terminal and one non terminal or only one terminal.
For example
S → 0A | 1B
A → 0C | 1A | 0
B → 1B | 1A | 1
C → 0 | 0A
This is an example of a regular grammar. Where 0 and 1 are the terminals and A, B, C, S are the non terminals. This RG (regular grammar) is a example of a Right Linear grammar as the Non terminals are on the right of the terminals.
This right linear grammar can be converted into a DFA as follows
1) Draw the corresponding states for all the non terminals S, A, B, C. Also include an extra state F which will be the final state.
2) From the first rule S → 0A | 1B, which means S on a 0 goes to A and S on a 1 goes to B.
3) From the second rule A → 0C | 1A | 0, which means A on a 0 goes to C, A on a 1 goes to back to A and if we comes across a terminal alone, like 0 in this case, it means that A on a 0 goes to the final state F.
4) From the third rule B → 1B | 1A | 0, which means B on a 1 goes back to B itself and also B on a 1 goes to A and B on a 0 goes to final state.
5) From the fourth rule C → 0 | 0A, C on a0 goes to final state and A.
As it can be seen, this is a NFA and can be converted to a DFA.
The table for this NFA is
0 | 1 | |
S | A | B |
A | C, F | A |
B | - | A, B, F |
C | A, F | - |
F | - | - |
The DFA table can be as follows,
0 | 1 | |
S (q0) | A | B |
A (q1) | C, F | A |
C,F (q2) | A, F | - |
B (q3) | - | A, B, F |
A,F (q4) | C, F | A |
A,B,F (q5) | C, F | A, B, F |
And the DFA will be
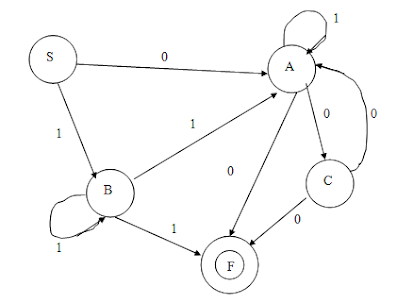
Right Linear grammar is where the Non terminal is on the right of the terminal. A FA of left linear grammar can be converted to FA of right linear grammar for the same RG.
In the previous example
S → 0A | 1B
A → 0C | 1A | 0
B → 1B | 1A | 1
C → 0 | 0A
This was the NFA for this RG.
To convert it to FA for right linear grammar
1) Reverse the first and last states and reverse all the arrows in the NFA or DFA or RG.
So the FA for this problem in right linear grammar will be
Feel free to comment if you have any doubts related to this topic.
Recommended articles:



Comments
Post a Comment