Moore and Mealy Machines

In finite automata, the acceptability of a string depends on whether we reach the final state or not. If we reach the final state output will be 1, otherwise output will be 0.

In a Moore and Mealy machine every input has an associated output with it.

Moore machine

Moore machine is defines as a 6 tuple {Q, Ʃ, δ, q₀, F, λ} where,

Q is a set of states

Ʃ is the input alphabet

δ is the transition table / diagram

q₀ is the start state

F is the set of final states

λ is the output alphabet

 In a Moore machine every state has a λ (output) associated with it. If you reach a state that has output 1 associated with it, the input is accepted. This machine is usually used in digital circuits.

For example we have to draw a Moore machine to count string ‘011’ in a sequence of numbers having 0’s and 1’s.

We have to give the output as 1 when we detect the string 011

1) If on q0 we get a 1, stay on q0. If on q0 we get a 0 go to q1, as the sequence 011 is getting formed. Output on q0 is 0

2) If on q1 we get a 0, stay at q1. If on q1 we get a 1, go to q2 with output on q1 as 0.

3) If on q2 we get a 0 go back to q1. If on q2 we get a 1, go to q3. Output on q3 is 0.  

4) If on q3 we get a 0 go back to q1 and if we get 1, go back to q0. And output at q3 will be 1 as the sequence 011 will be detected.

	0	1	Output
q0	q1	q0	0
q1	q1	q2	0
q2	q1	q3	0
q3	q1	q0	1

Mealy machine

Mealy machine is also a 6 tuple {Q, Ʃ, δ, q₀, F, λ} where,

Q is a set of states

Ʃ is the input alphabet

δ is the transition table / diagram

q₀ is the start state

F is the set of final states

λ is the output alphabet

 In a Mealy machine every transition has a λ (output) associated with it. If you make a transition that has output 1 associated with it, the input is accepted. This machine is also used in digital circuits.

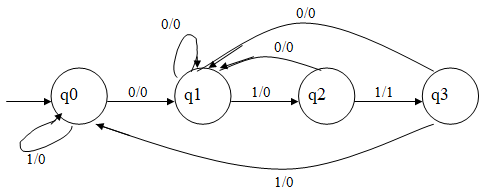
 For the same example of counting string 011 the Mealy circuit would be as follows

1) When on q0 if we get a 1, output is 0 and we stay on q0. If we get a 0 on q0, output is 0 and we go to q1.

2) When on q1 if we get a 0, output is 0 and we stay at q1. If we get a 1 on q1, output is 0 and we go to q2.

3) When on q2 if we get a 0, output is 0 and we go to q1. If we get a 1 on q2, output is 1 and we go to q3. The string is found here.

4) When on q3 if we get a 0, output is 0 and we go to q1. If we get a 1 output is 0 and we go to q0.

	0		1
	state                   output		state                 output
q0	q1	0	q0	0
q1	q1	0	q2	0
q2	q1	0	q3	1
q3	q1	0	q0	0

Another example

Draw a Mealy and Moore machine to find the one’s complement of a binary number

Moore machine

1) If on q0 we get a 0, go to q1 with output 1. If on q0 we get a 1, go to q2 and output will be 0.

2) If on q1 we get a 0 stay on same state and output will be 1. If on q1 we get a 1, go to q2 and output will be 0.

3) if on q2 we get a 1, we stay a q2 and output will be 0. If we get a 0 on q2, go to q1 and output will be 1.

	0	1	Output
q0	q1	q2	0
q1	q1	q2	1
q2	q1	q2	0

Mealy machine

1) On q0, when we get a 0, stay at q0 and output is 1. if we get 1, stay at q0 and output is 0

	0		1
	state                   output		state                output
q0	q0	1	q0	0

Another example

Draw a mealy machine for a binary number incrementer

1) When on q0, if we get a 1, go to q1 and output is 0 as in binary addition 1+1=0 and carry is generated. (q1 is the state for carry)

2) When on q0 if we get a 1, go to q2 and output is 1 as 1+0=1 and no carry is generated.( q2 is the state for no carry)

3) At q1 if we get a 1, stay at the same state and output is 0, again carry is generated. If we get a 0 at q0, go to qo and output is 1 as no carry is generated.

4) When on q2 if we get a 0, stay at the same state and output is 0 and if input is 1, output is also 1 and stay at the same state.

	0		1
	state                 output		state                output
q0	q2	1	q1	0
q1	q2	1	q1	0
q2	q2	0	q2	1

Feel free to comment below, if you still have some doubts. 

Recommended articles:

Introduction to Finite Automata

Deterministic and Non deterministic Finite Automata